|
Lambertian Reflectance, Lambertian Radiator
This article is a list of things named in the memory of the 18th century Swiss scientist Johann Heinrich Lambert: Optics * Beer–Lambert law **Beer–Lambert–Bouguer law, see above * lambert (unit) **Foot-lambert * Lambert's cosine law * Lambertian reflectance Mathematics * Lambert azimuthal equal-area projection * Lambert conformal conic projection * Lambert cylindrical equal-area projection * Lambert mean * Lambert quadrilateral * Lambert series * Lambert summation * Lambert W function * Lambert's problem * Lambert's theorem on the parabola * Lambert's trinomial equation * Lambertian function (inverse of the Gudermannian function) Other * 187 Lamberta, asteroid * Lambert (lunar crater). In the MARE IMBRIUM, Diameter: 30.1209 km * Lambert (Martian crater) Lambert may refer to People *Lambert (name), a given name and surname * Lambert, Bishop of Ostia (–1130), became Pope Honorius II * Lambert, Margrave of Tuscany (fl. 929–931), also count and duke of Lucca *Lamb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johann Heinrich Lambert
Johann Heinrich Lambert (; ; 26 or 28 August 1728 – 25 September 1777) was a polymath from the Republic of Mulhouse, at that time allied to the Switzerland, Swiss Confederacy, who made important contributions to the subjects of mathematics, physics (particularly optics), philosophy, astronomy and map projections. Biography Lambert was born in 1728 into a Huguenot family in the city of Mulhouse, nowadays in Alsace, France, at that time a city-state allied to the Swiss Confederacy. Some sources give 26 August as his birth date and others 28 August. Leaving school at 12, he continued to study in his free time while undertaking a series of jobs. These included assistant to his father (a tailor), a clerk at a nearby iron works, a private tutor, secretary to the editor of ''Basler Zeitung'' and, at the age of 20, private tutor to the sons of Count Salis in Chur. Travelling Europe with his charges (1756–1758) allowed him to meet established mathematicians in the German states, Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert Series
In mathematics, a Lambert series, named for Johann Heinrich Lambert, is a series taking the form :S(q)=\sum_^\infty a_n \frac . It can be resummed formally by expanding the denominator: :S(q)=\sum_^\infty a_n \sum_^\infty q^ = \sum_^\infty b_m q^m where the coefficients of the new series are given by the Dirichlet convolution of ''a''''n'' with the constant function 1(''n'') = 1: :b_m = (a*1)(m) = \sum_ a_n. \, This series may be inverted by means of the Möbius inversion formula, and is an example of a Möbius transform. Examples Since this last sum is a typical number-theoretic sum, almost any natural multiplicative function will be exactly summable when used in a Lambert series. Thus, for example, one has :\sum_^\infty q^n \sigma_0(n) = \sum_^\infty \frac where \sigma_0(n)=d(n) is the number of positive divisors of the number ''n''. For the higher order sum-of-divisor functions, one has :\sum_^\infty q^n \sigma_\alpha(n) = \sum_^\infty \frac = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert (lunar Crater)
Lambert is a lunar impact crater on the southern half of the Mare Imbrium basin. It was named after Swiss polymath Johann Heinrich Lambert. It lies to the east and somewhat south of the slightly larger crater Timocharis. To the south is the smaller Pytheas, and some distance to the west-southwest is Euler. The crater is relatively easy to locate due to its isolated position on the mare. It has an outer rampart, terraced inner walls, and a rough interior that has a comparable albedo to its surroundings. Instead of a central peak, a small craterler lies at the midpoint of the interior. Just to the south of Lambert's ramparts is the lava-covered rim of Lambert R, a crater that is almost completely covered by the mare. The diameter of this ghost crater is larger than Lambert, but it is difficult to spot except when the Sun is at a very low angle, casting long shadows. Lambert is a crater of Eratosthenian age. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
187 Lamberta
187 Lamberta is a main-belt asteroid that was discovered by Corsican-born French astronomer Jérôme Eugène Coggia on April 11, 1878, and named after the astronomer Johann Heinrich Lambert. It was the second of Coggia's five asteroid discoveries. The spectrum matches a classification of a C-type asteroid, which may mean it has a composition of primitive carbonaceous materials. It is a dark object as indicated by the low albedo Albedo ( ; ) is the fraction of sunlight that is Diffuse reflection, diffusely reflected by a body. It is measured on a scale from 0 (corresponding to a black body that absorbs all incident radiation) to 1 (corresponding to a body that reflects ... and has an estimated size of about 131 km. Notes References External links * * Background asteroids Lamberta Lamberta C-type asteroids (Tholen) Ch-type asteroids (SMASS) 18780411 {{C-beltasteroid-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
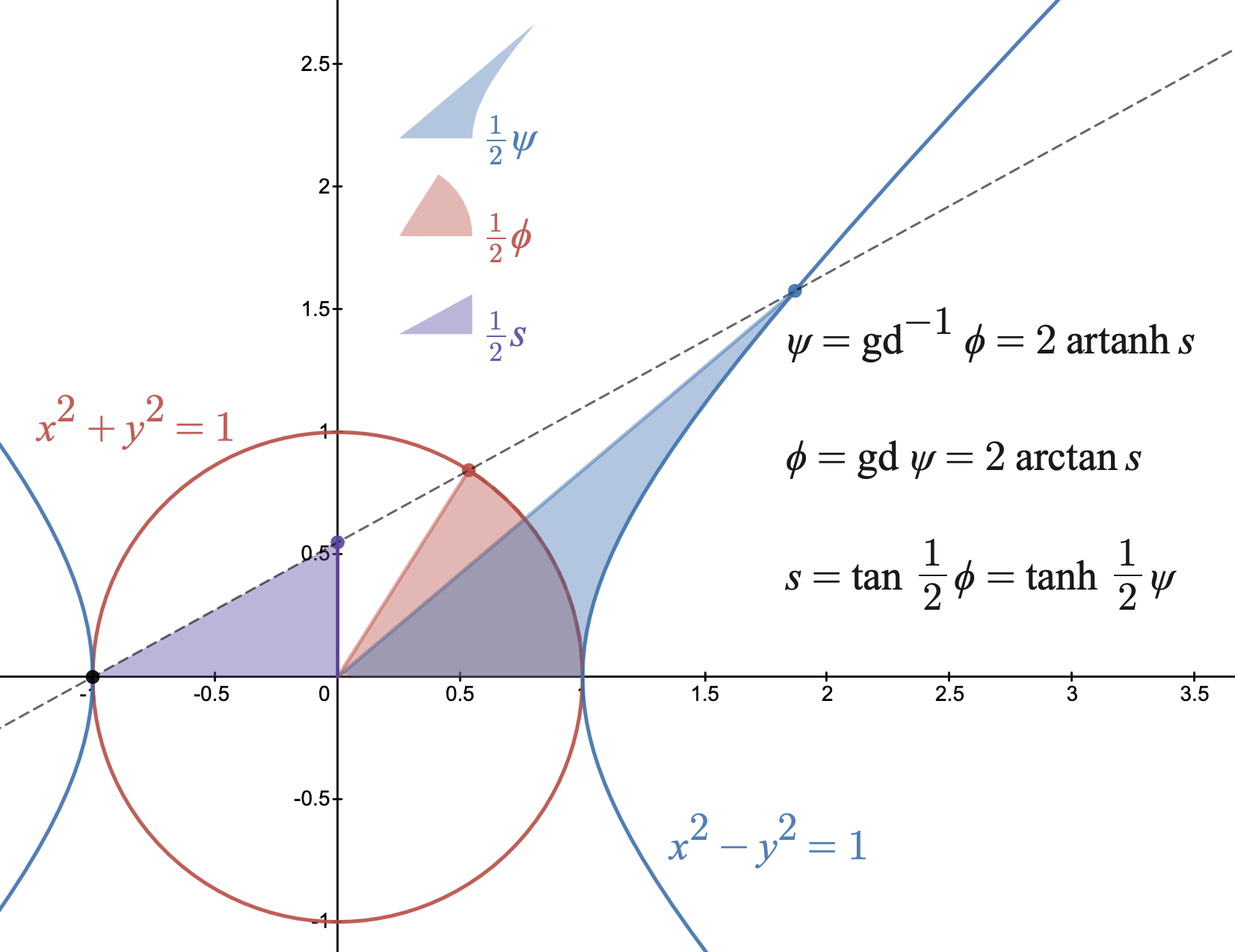
Gudermannian Function
In mathematics, the Gudermannian function relates a hyperbolic angle measure \psi to a circular angle measure \phi called the ''gudermannian'' of \psi and denoted \operatorname\psi. The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude \operatorname(\psi, m) when parameter m=1. The real Gudermannian function is typically defined for -\infty < \psi < \infty to be the integral of the hyperbolic secant : The real inverse Gudermannian function can be defined for |
Trinomial
In elementary algebra, a trinomial is a polynomial consisting of three terms or monomials. Examples of trinomial expressions # 3x + 5y + 8z with x, y, z variables # 3t + 9s^2 + 3y^3 with t, s, y variables # 3ts + 9t + 5s with t, s variables # ax^2+bx+c, the quadratic polynomial in standard form with a,b,c variables.Quadratic expressions are not always trinomials, the expressions' appearance can vary. # A x^a y^b z^c + B t + C s with x, y, z, t, s variables, a, b, c nonnegative integers and A, B, C any constants. # Px^a + Qx^b + Rx^c where x is variable and constants a, b, c are nonnegative integers and P, Q, R any constants. Trinomial equation A trinomial equation is a polynomial equation involving three terms. An example is the equation x = q + x^m studied by Johann Heinrich Lambert in the 18th century. Some notable trinomials * The quadratic trinomial in standard form (as from above): :: ax^2+bx+c * sum or difference of two cubes: :: a^3 \pm b^3 = (a \pm b)(a^2 \mp ab + b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactly the same curves. One description of a parabola involves a Point (geometry), point (the Focus (geometry), focus) and a Line (geometry), line (the Directrix (conic section), directrix). The focus does not lie on the directrix. The parabola is the locus (mathematics), locus of points in that plane that are equidistant from the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane (geometry), plane Parallel (geometry), parallel to another plane that is tangential to the conical surface. The graph of a function, graph of a quadratic function y=ax^2+bx+ c (with a\neq 0 ) is a parabola with its axis parallel to the -axis. Conversely, every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert's Problem
In celestial mechanics, Lambert's problem is concerned with the determination of an orbit from two position vectors and the time of flight, posed in the 18th century by Johann Heinrich Lambert and formally solved with mathematical proof by Joseph-Louis Lagrange. It has important applications in the areas of rendezvous, targeting, guidance, and preliminary orbit determination. Suppose a body under the influence of a central gravitational force is observed to travel from point ''P''1 on its conic trajectory, to a point ''P''2 in a time ''T''. The time of flight is related to other variables by Lambert's theorem, which states: :''The transfer time of a body moving between two points on a conic trajectory is a function only of the sum of the distances of the two points from the origin of the force, the linear distance between the points, and the semimajor axis of the conic.'' Stated another way, Lambert's problem is the boundary value problem for the differential equation \ddot = - ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert W Function
In mathematics, the Lambert function, also called the omega function or product logarithm, is a multivalued function, namely the Branch point, branches of the converse relation of the function , where is any complex number and is the exponential function. The function is named after Johann Heinrich Lambert, Johann Lambert, who considered a related problem in 1758. Building on Lambert's work, Leonhard Euler described the function per se in 1783. For each integer there is one branch, denoted by , which is a complex-valued function of one complex argument. is known as the principal branch. These functions have the following property: if and are any complex numbers, then : w e^ = z holds if and only if : w=W_k(z) \ \ \text k. When dealing with real numbers only, the two branches and suffice: for real numbers and the equation : y e^ = x can be solved for only if ; yields if and the two values and if . The Lambert function's branches cannot be expressed in terms o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert Summation
In mathematical analysis and analytic number theory, Lambert summation is a summability method for summing infinite series related to Lambert series specially relevant in analytic number theory. Definition Define the Lambert kernel by L(x)=\log(1/x)\frac with L(1)=1. Note that L(x^n)>0 is decreasing as a function of n when 0 Abelian and Tauberian theorem Abelian theorem: If a series is convergent to then it is Lambert summable to . : Suppose that is Lambert summable to |
Lambert Quadrilateral
In geometry, a Lambert quadrilateral (also known as Ibn al-Haytham–Lambert quadrilateral), is a quadrilateral in which three of its angles are right angles. Historically, the fourth angle of a Lambert quadrilateral was of considerable interest since if it could be shown to be a right angle, then the Euclidean parallel postulate could be proved as a theorem. It is now known that the type of the fourth angle depends upon the geometry in which the quadrilateral exists. In hyperbolic geometry the fourth angle is Acute angle, acute, in Euclidean geometry it is a right angle and in elliptic geometry it is an obtuse angle. A Lambert quadrilateral can be constructed from a Saccheri quadrilateral by joining the midpoints of the base and summit of the Saccheri quadrilateral. This line segment is perpendicular to both the base and summit and so either half of the Saccheri quadrilateral is a Lambert quadrilateral. Lambert quadrilateral in hyperbolic geometry In hyperbolic geometry a Lamber ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beer–Lambert Law
The Beer–Bouguer–Lambert (BBL) extinction law is an empirical relationship describing the attenuation in intensity of a radiation beam passing through a macroscopically homogenous medium with which it interacts. Formally, it states that the intensity of radiation decays exponentially in the absorbance of the medium, and that said absorbance is proportional to the length of beam passing through the medium, the concentration of interacting matter along that path, and a constant representing said matter's propensity to interact. The extinction law's primary application is in chemical analysis, where it underlies the Beer–Lambert law, commonly called Beer's law. Beer's law states that a beam of visible light passing through a chemical solution of fixed geometry experiences absorption proportional to the solute concentration. Other applications appear in physical optics, where it quantifies astronomical extinction and the absorption of photons, neutrons, or rarefied gas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |